[이해하기] 탐색으로 문제 해결하기
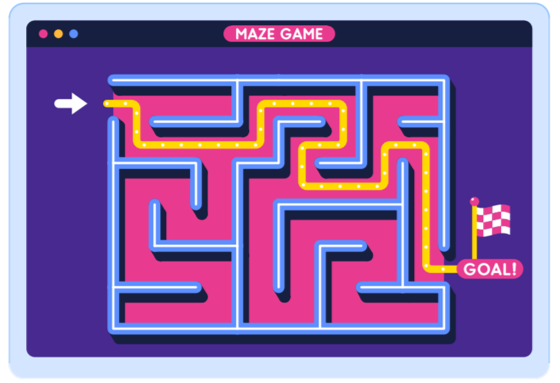
미로찾기

위의 미로 찾기 퍼즐을 한 번 풀어보세요. 어때요, 길을 찾으셨나요? 미로 찾기는 우리가 살면서 한 번쯤은 접해보았을 친숙한 문제입니다. 복잡한 길을 찾아 출발점에서 시작해서 도착점까지 도달하는 퍼즐이지요.
여러분은 미로 찾기를 할 때 어떻게 길을 찾았나요? 어떤 방법으로 길을 찾을지 생각해두고 퍼즐을 풀지 않았어도, 분명 여러분이 퍼즐을 해결한 데에는 여러분만의 문제 해결하는 방법이 있었을 겁니다. 여러분이 어떤 흐름으로 퍼즐을 풀었는지 잠시 생각해보고, 자신이 문제를 해결한 규칙을 친구들의 방법과 비교해보세요.
컴퓨터도 여러분처럼 미로 찾기 문제를 해결할 수 있답니다. 컴퓨터는 이러한 문제를 어떻게 해결할 수 있을까요? 컴퓨터가 미로 찾기 문제를 해결하는 방법도 여러분의 방법과 비슷할까요? 이제부터 컴퓨터가 이와 같은 문제를 해결하는 방법을 함께 알아봅시다.
<미로 찾기>
Q. 출발점에서 도착점까지 가는 길을 어떤 방법으로 찾았나요? 친구와 이야기를 나누어보고, 서로의 방법을 비교해봅시다.
탐색과 문제해결

여러분 오목 게임을 해본 적이 있나요? 오목을 둘 때 자신의 차례가 되면 위의 그림처럼 머릿속으로 바둑돌 위치에 따라 결과가 어떻게 될지, 어디에 내 바둑돌을 놓는 것이 유리한지를 생각하면서 게임을 할 겁니다. 즉, 여러분의 바둑돌을 놓을 수 있는 많은 곳들 중 가장 좋은 곳이 어디인지를 생각합니다. 이처럼 여러 개의 후보들 중에서 더 좋은 것을 찾는 것을 ‘탐색’이라고 합니다. 이번 주제에서는 문제해결, 그중에서도 탐색을 통한 문제 해결에 대해 알아보려고 합니다.
먼저 문제해결이란 무엇일까요? 보통 ‘문제 상황’이라는 것은 내가 원하는 모습(목표 상태)과 지금 모습(시작 상태) 사이에 차이가 있는 것을 말합니다. 그리고 ‘문제해결’이란 시작 상태에서 목표 상태까지 순서대로 어떤 과정을 거쳐 찾아가는 것을 뜻합니다. 예를 들어, 앞에서 살펴본 미로 찾기의 문제해결은 출발점(시작 상태)에서 도착점(목표 상태)까지 순서대로 길을 찾아가는 것이죠. 오목 두기에서는 처음에 바둑돌이 아무것도 없는 상태(시작 상태)에서 시작하여 내가 이기게 되는 상태(목표 상태)까지 차례대로 방법을 찾아가는 과정입니다.
컴퓨터가 탐색을 통해 문제를 해결하기 위해서는 두 가지 단계가 필요합니다. 바로 문제 표현하기(2-1)와 탐색하기(2-2)입니다. 강 건너기 문제를 통해 좀 더 자세히 알아봅시다.
2. 강 건너기 문제 해결하기

사람이 늑대, 양, 양배추를 싣고 강을 건너려고 합니다. 여기서 중요한 조건이 있습니다. 배에는 사람 외에 단 한 가지만 더 실을 수 있습니다. 그런데 늑대가 양과 단둘이 있으면 늑대는 양을 잡아 먹어버리고, 양과 양배추가 단둘이 있으면 양이 양배추를 다 먹어버립니다. 이런 조건을 모두 생각하면서 모든 것을 안전하게 옮기려면 최소 몇 번 강을 건너야 할까요?
2-1. 문제 표현하기
|
강 건너기 문제를 해결하기 위해서 다음과 같이 문제 상황을 간단히 표현하겠습니다. 오른쪽와 같이 동그라미의 왼쪽은 강을 건너기 전 출발지에 남아 있는 것을, 오른쪽에는 강을 건너 도착지에 넘어간 것을 표시합니다. |
|
그리고 한 동그라미에서 다음 동그라미로 이동하는 것은 화살표로 표현하고, 화살표가 그어질 때마다 강을 한 번 건넌 것을 의미합니다. |
2-2. 탐색 및 문제 해결하기
Q. 강 건너기 문제를 위에서 살펴본 문제 표현 방식으로 탐색을 이용하여 해결해봅시다.
Q. 처음 시작 상태(모두 출발지에 있는 것)에서 목표 상태(모두 도착지에 있는 것)까지 가는 순서를 이야기해봅시다.
Q. 자신이 찾은 순서와 친구들이 찾은 순서를 서로 비교해봅시다.
모든 것을 안전하게 옮기기 위한 순서를 잘 찾았나요? 이렇게 시작 상태에서 목표 상태까지 가는 순서를 '경로'라고 합니다. 문제를 해결하기 위한 경로는 여러 개가 생길 수 있습니다. 그렇다면 여러 가지 경로 중에 어떤 것을 선택하는 것이 좋을까요? 맞습니다. 가장 빠르게 문제를 해결하는 경로를 찾는 것이 좋겠죠.
탐색 알고리즘 중에서는 사람의 지식과 경험을 사용하여 가장 빠른 경로를 효율적으로 찾는 것이 있습니다. 이것을 '휴리스틱 탐색'이라고 합니다. 탐색 알고리즘 중에서도 사람의 지식과 경험을 녹여 만든 휴리스틱 탐색은 인공지능의 영역이라고 할 수 있습니다. 인공지능은 사람이 가진 지적인 능력을 컴퓨터로 구현한 것이기 때문입니다. 휴리스틱 탐색 알고리즘을 사용하면 미로 찾기도 금방 해결할 수 있고, 오목 게임도 이길 수 있게 됩니다.
3. 탐색을 통한 문제해결 적용 사례
강 건너기 문제를 잘 해결하셨나요? 우리의 생활 속 문제 중에는 강 건너기 문제와 같이 탐색을 통해 해결할 수 있는 문제들이 많이 있습니다. 탐색을 통해 문제를 해결하는 인공지능 프로그램의 사례를 함께 살펴봅시다.
3-1. 내비게이션

내비게이션은 현재 위치에서 목적지까지 가는 많은 경로들 중 가장 효율적인 길을 탐색하여 알려줍니다. 최근의 내비게이션은 탐색 알고리즘 외에도 다양한 기술이 포함되어 있지만, 기본적인 원리는 휴리스틱 탐색에 기초를 두고 있습니다.
3-2. 체스 프로그램 딥 블루

오목 게임을 탐색 알고리즘으로 해결할 수 있듯이, 체스 경기도 그렇게 할 수 있답니다. 딥 블루는 탐색 알고리즘으로 만들어진 체스 프로그램으로, 1997년 세계 체스 챔피언을 이긴 최초의 컴퓨터입니다.
바둑 역시 이러한 탐색 알고리즘을 이용한 인공지능 프로그램을 만들었는데, 최근에 나온 알파고는 여기에 추가로 기계학습 기법도 합쳐져서 아주 강력한 인공지능이 되었습니다. 기계학습이 무엇인지는 나중에 함께 알아보겠습니다.
3-3. 미로 찾기 인공지능
|
미로 찾기 인공지능은 출발점에서 갈 수 있는 다양한 경로들 중 도착지로 향하는 가장 빠른 길을 탐색합니다. 미로 찾기 문제는 다양한 탐색 알고리즘으로 해결할 수 있습니다. |
※ 휴리스틱 탐색
우리의 강 건너기 문제는 탐색할 경로의 수가 엄청 많지 않았습니다. 그런데 만약 우리가 탐색해야 하는 경우의 수가 수천억 개 혹은 그 이상으로 넘어가면 어떨까요? 컴퓨터를 이용해 계산한다고 하더라도 이는 엄청나게 많은 시간이 필요할 것입니다. 그래서 이런 탐색의 시간을 줄이기 위해 사용되는 방법들이 있는데 이 중 하나가 바로 휴리스틱 탐색입니다. 휴리스틱 탐색은 탐색하는 시간을 줄이기 위해 사람이 이미 알고 있는 경험적 지식을 사용합니다.
휴리스틱 탐색에서는 가장 좋은 다음 경로가 무엇인지 계산하여 가장 최적의 다음 경로를 찾습니다. 이렇게 차례 차례 한 단계씩 가면서 최종적으로 목표지점에 도달하는 것을 목표로 합니다. 휴리스틱 탐색에서는 모든 경로를 탐색하지 않고 효율적인 경로를 우선으로 탐색하기 때문에 훨씬 더 빠르게 목표지점에 도달할 수 있습니다.
틱택토 게임(삼목 게임)을 통해 휴리스틱 탐색을 알아봅시다.

틱택토 게임에서 승리할 수 있는 선이 몇 개 인지 세 봅시다. (1)과 같이 놓았을 때는 승리할 수 있는 승리선은 3개가 나옵니다. (2)와 같이 놓았을 때는 승리선은 4개가 나오기 때문에 (1)보다 (2)가 더 이길 확률이 높은 선택이라고 할 수 있습니다. 이것은 휴리스틱, 즉 사람의 경험적 지식의 예시 중 하나입니다. 같은 문제라도 여러 가지 다른 휴리스틱이 있을 수 있습니다. 이처럼 휴리스틱을 사용하여 내 차례에서 내가 이길 수 있는 가능성이 큰 것을 효율적으로 선택하여 문제를 해결하는 것이 휴리스틱 탐색입니다.
4. 틱택토(Tic-Tac-Toe) 게임
탐색의 원리를 생각하며 틱택토 게임을 해봅시다.
<게임 규칙>
9개의 칸 위에 한 명은 O를, 한 명은 X를 번갈아가며 그립니다. 먼저 O나 X를 3개가 직선으로 이어지게 만드는 사람이 승리합니다.
예) 왼쪽과 같은 상황이면 X 가 승리
※ 이번 시간에 배운 내용을 생각 그물로 표현하여 정리해봅시다.